卫星信号串行捕获

信号捕获的基本概念

GNSS接收机的数字部分要完成跟踪和解码工作，就必须将自己所接收到的卫星信号与其他不同的卫星信号中区分出来，而卫星信号捕获电路便是实现这一功能的模块电路。总的来说，信号捕获需要完成以下三个功能：1.识别出所接收的卫星信号所采用的伪码从而实现卫星区分。2.从接收到的卫星信号中提取出信号传输过程中的多普勒频偏的估计值。3.从接收到的卫星信号中得到其伪码与本地伪码之间的初步码相位差值。由此可见，捕获其实是一个二维搜索过程，不仅要搜索伪码相位，还要搜索多普勒频移。即捕获的目的是确定能够观测到的卫星，并且估计出粗略的码相位和载波多普勒频移。

传统的接收机捕获算法采用串行捕获技术，即将接收到的信号与本地产生的参考信号进行自相关，当搜索到最大相关输出大于阈值时即判断捕获到该卫星。串行捕获算法的结构接单且容易用硬件实现，但运算量非常大，但这一捕获算法就理论研究来说还是有一定的研究价值。

串行捕获算法的流程框图

串行捕获算法的具体流程图如下所示：

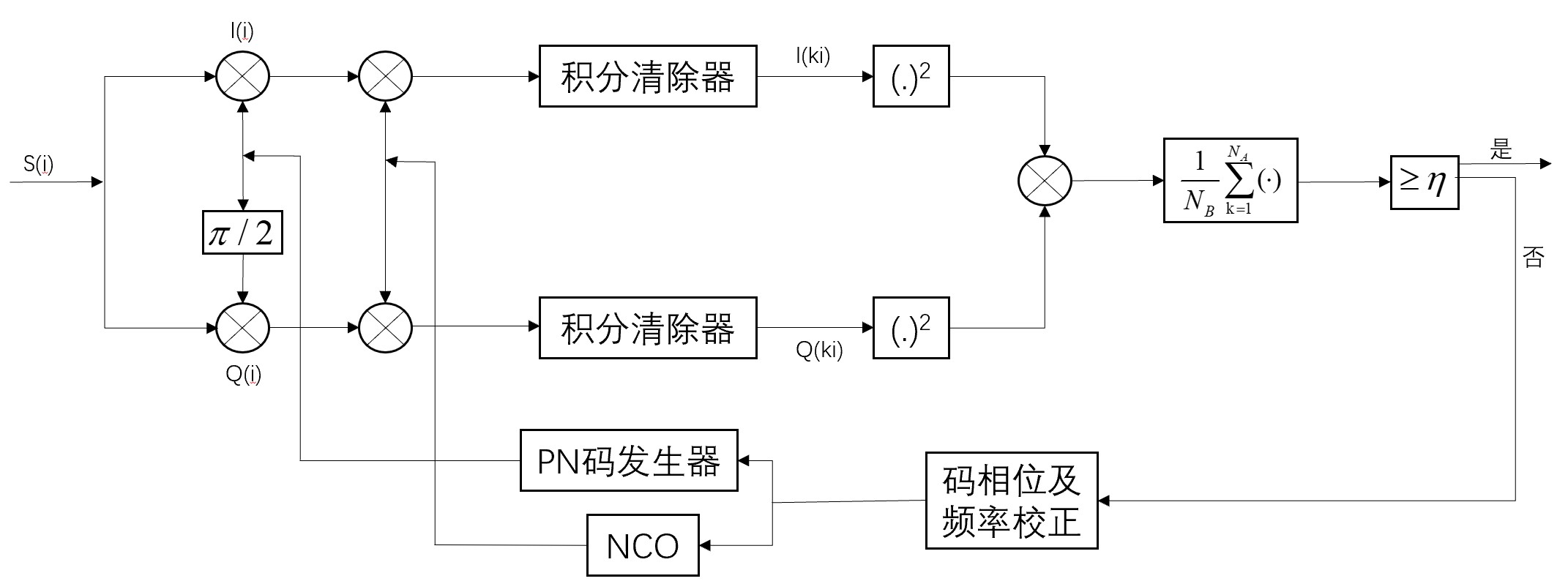
假设接收到的模拟信号S(t)为$S(t)=A\cdot C(t)\cdot cos[2\pi(f_b+f_d)t+\phi]+n(t)$，其中$f_b$为基带载波频率，$f_d$为多普勒频偏。则有数字抽样信号$S(i)=A\cdot C(iT_s)\cdot cos[(\omega_b+\omega_d)i+\phi]+n(i)$，$\omega_b=2\cdot \pi f_bT_s$，$\omega_d=2\cdot \pi f_dT_s$为数字角频率。设本地I路载波为$I(i)=2cos[(\omega_b+\omega_d)i+\phi]$，Q路载波为$Q(i)=2sin[(\omega_b+\omega_d)i+\phi]$，本地伪码为：$\hat{C}(i)=C(iT_s-\hat{\tau})$，$\hat{\tau}$为测距所需的伪码延迟。经积分清除后有：

$$I(k)=A\cdot R(\hat{\tau})\cdot sin(\Delta\omega_d \cdot N/2) \cdot cos[(\Delta\omega_d \cdot N/2)+\Delta\phi+\Delta\omega_d\cdot N\cdot k] \\ Q(k)=A\cdot R(\hat{\tau})\cdot sin(\Delta\omega_d \cdot N/2) \cdot sin[(\Delta\omega_d \cdot N/2)+\Delta\phi+\Delta\omega_d\cdot N\cdot k]$$

其中，$\Delta\omega_d=\omega_d-\hat{\omega_d}$，$\Delta\phi=\phi=\hat{\phi}$，N为数字积分清除器的积分点数，也即子相关器相关点数，$R(\hat{\tau})$为码相关值均值，其值为$R(\hat{\tau})=E[\frac{1}{N}\sum_{i=(k-1)N}^{kN-1}{C(iT_s)\cdot C(iT_s-\hat{\tau})}]$经平方律检波后求和，得判别捕获的检测统计量为：$Z=\sum_{k=i}^{N_B}{[I^2(K)+Q^2(k)]}$，$N_B$为视频累计点数，$\eta$为捕获判决门限。

串行捕获仿真

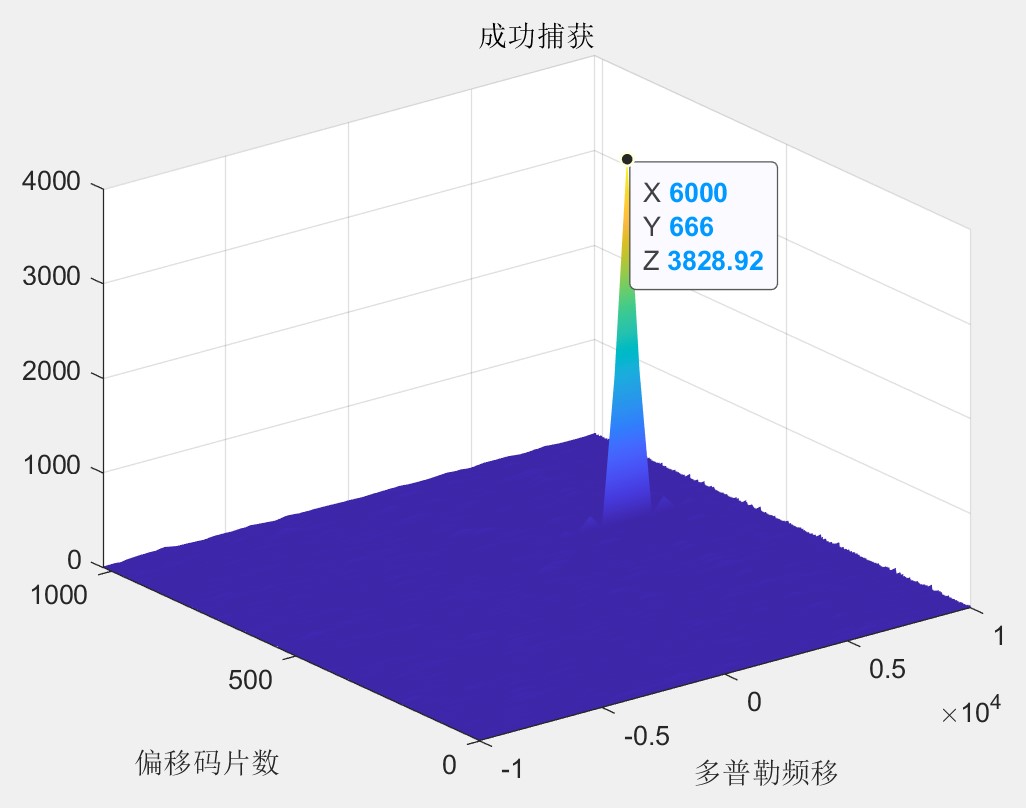
对串行捕获进行MATLAB仿真时设置多普勒频偏为6kHz，伪码相位延迟为666个码片延迟，本地生成两种CA码模拟本地已知的两个卫星伪码，接收的卫星信号为其中一颗卫星所发射的信号，则仿真结果如下所示：

当本地伪码与所接收的卫星信号扩频所采用的伪码不一致时，此时串行捕获电路无法成功捕获到相应的卫星信号，仿真结果图如下所示：

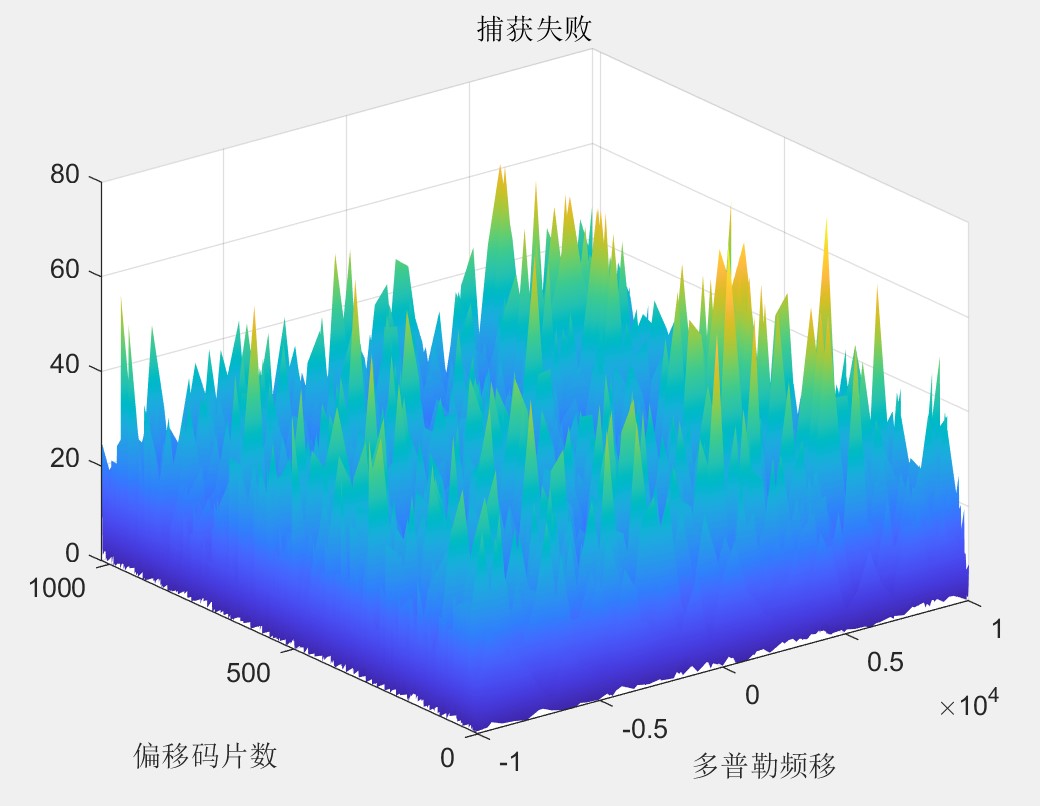
当本地伪码与所接收的卫星信号采用的扩频码一致时，串行捕获电路会计算得出最大的相关峰，并获得所接收的卫星信号的多普勒频偏以及相应的码片延迟数，值得注意的是捕获电路所得的多普勒频偏以及码片延迟均为粗略估计，具有一定的误差，因此只能作为后续所需的信号跟踪环路的输入值帮助实现载波及码片跟踪从而获得更精确的多普勒频偏以及码片延迟数，仿真结果图如下所示：

clc;clear;close all;
f_clk=1.023e6;    %寄存器时钟脉冲频率即码片速率
fs=f_clk*60;    %系统仿真采样率设定
t=0:(1/fs):((1e-3)-1/fs);    %系统仿真时间设定(1ms)
f_i=f_clk*10;    %输入的数字中频频率
fd_i=6e3;    %多普勒频偏
fd_step=-10e3:500:10e3;    %频率搜索步长
code_phase_move=666;    %伪码相位延迟
code_phase_step=0:1:1022;    %伪码相位搜索步长
tags = [[2 6];[3 7];[4 8];[5 9];[1 9];[2 6];[1 8];[2 9];[3 10];[2 3];...
    [3 4];[5 6];[6 7];[7 8];[8 9];[9 10];[1 4];[2 5];[3 6];[4 7];...
    [5 8];[6 9];[1 3];[4 6];[5 7];[6 8];[7 9];[8 10];[1 6];[2 7];...
    [3 8];[4 9]];    %G2码相位选择

[wave_CA_1,code_CA_1]=CAcode_generation(tags(6,:),f_clk,[t(1),t(end)],fs);    %本地伪码1
[wave_CA_2,code_CA_2]=CAcode_generation(tags(12,:),f_clk,[t(1),t(end)],fs);    %本地伪码2
wave_carrier_transmit=cos(2*pi*(f_i+fd_i)*t);
wave_transmit=circshift(wave_CA_1,round(-(1+(code_phase_move/f_clk-t(1))*fs))).*wave_carrier_transmit;    %捕获电路输入信号
capture_result_1=zeros(length(fd_step),length(code_phase_step));
capture_result_2=zeros(length(fd_step),length(code_phase_step));
for i1=1:length(fd_step)
    wave_carrier_receive_I=cos(2*pi*(f_i+fd_step(i1))*t);
    wave_carrier_receive_Q=sin(2*pi*(f_i+fd_step(i1))*t);
    for i2=1:length(code_phase_step)
        wave_CA_phase_1=circshift(wave_CA_1,round(-(1+(code_phase_step(i2)/f_clk-t(1))*fs)));
        wave_CA_phase_2=circshift(wave_CA_2,round(-(1+(code_phase_step(i2)/f_clk-t(1))*fs)));
        R_I_1=wave_transmit.*wave_carrier_receive_I.*wave_CA_phase_1;
        R_Q_1=wave_transmit.*wave_carrier_receive_Q.*wave_CA_phase_1;
        R_I_2=wave_transmit.*wave_carrier_receive_I.*wave_CA_phase_2;
        R_Q_2=wave_transmit.*wave_carrier_receive_Q.*wave_CA_phase_2;
        NB=1;    %判决视域点数
        N=round(length(R_I_1)/NB);    %相干积分点数
        R_I_sum_1=zeros(1,NB);
        R_Q_sum_1=zeros(1,NB);
        R_I_sum_2=zeros(1,NB);
        R_Q_sum_2=zeros(1,NB);
        for i3=1:NB
            index_1=(i3-1)*N+1;
            index_2=i3*N;
            R_I_sum_1(i3)=sum(R_I_1(index_1:index_2));
            R_Q_sum_1(i3)=sum(R_Q_1 (index_1:index_2));
            R_I_sum_2(i3)=sum(R_I_2(index_1:index_2));
            R_Q_sum_2(i3)=sum(R_Q_2(index_1:index_2));
        end
        M_I_1=R_I_sum_1.^2;
        M_Q_1=R_Q_sum_1.^2;
        M_I_2=R_I_sum_2.^2;
        M_Q_2=R_Q_sum_2.^2;
        capture_result_1(i1,i2)=(sum(M_I_1)+sum(M_Q_1))/N;
        capture_result_2(i1,i2)=(sum(M_I_2)+sum(M_Q_2))/N;
    end
end
%%
[FD,PHASE_code]=meshgrid(fd_step,code_phase_step);%fd_step code_phase_step
figure;
surf(FD,PHASE_code,capture_result_1');shading interp;
xlabel("多普勒频移");
ylabel("偏移码片数");
title("成功捕获");
figure;
surf(FD,PHASE_code,capture_result_2');shading interp;
xlabel("多普勒频移");
ylabel("偏移码片数");
title("捕获失败");

function [wave,code]=CAcode_generation(phase_tag,F_CLK,T,FS)
%参数说明：
%输入：phase_tag(G2码相位选择参数)，F_CLK(码片速率设置)，
% T(系统仿真时间设定T(1)为仿真时间零点，T(2)为仿真时间终点)，FS为系统采样频率)
% 实际输出的伪码波形对应的时间横坐标为：t=[T(1):(1/fs):(T(2)-1/fs)];
%输出：wave(伪码时域波形)，code(伪码二进制序列)
    reg_G1=-ones(1,10);    %-1代表1，1代表0
    reg_G2=-ones(1,10);    
    index_code=0;
    t_chip=1/F_CLK;
    wave=zeros(1,(T(2)+1/FS)*FS);
    code=zeros(1,(T(2)+1/FS)*F_CLK);
    for i0=1:(T(2)+1/FS)*FS
        if ((T(1)+(i0-1)/FS)>=T(1)+index_code*t_chip)
            sum_G1=reg_G1(3)*reg_G1(10);
            reg_G1(2:10)=reg_G1(1:9);
            reg_G1(1)=sum_G1;
            sum_G2=reg_G2(2)*reg_G2(3)*reg_G2(6)*reg_G2(8)*reg_G2(9)*reg_G2(10);
            reg_G2(2:10)=reg_G2(1:9);
            reg_G2(1)=sum_G2;
            index_code=index_code+1;
            code(index_code)=reg_G1(10)*reg_G2(phase_tag(1))*reg_G2(phase_tag(2));
        end
        wave(i0)=code(index_code);
    end
%     wave=-wave;
%     code=-code;
end

值得讨论的捕获问题

(1)提高捕获速度的方法：重新采样，减少计算数据个数；增加搜索频率的步长；但这两办法都将降低信噪比，但采用非相干捕获，最后还是可以找出相关峰值。此外，由于计算量的限制，在搜索信号时一次只有一个通道进行捕获，即不能同时所有通道都捕获卫星。因为若多通道捕获，由于捕获占用的计算资源多可能会造成无法实时跟踪，不符合系统设置的实时性要求。
(2)频率搜索步长的设定也非常重要，步长的选定需要确保输入信号和本地产生的载波再生信号相差小于1个载波周期，来确保二者存在一定的相关性。
(3)捕获电路采样时长选定同样重要，一方面采样时长会影响频率搜索步长，另一方面采样时长不能超过导航电文数据翻转时间的一半。
(4)采用非相干积分，即每毫秒的捕获结果进行累加，由于噪声累加的结果增大不如信号累加的结果增大的快，使得经过一段时间后，可找出最大相关峰。
(5)检测判决算法也很重要，影响系统信号捕获的虚警和漏警概率，不同的检测判决策略也值得仔细推敲。