并行捕获的基本概念

串行频率捕获是在码片延迟与多普勒频偏这两个维度上进行捕获搜索，这样无疑会加长捕获运算的时间，因此相应的并行捕获算法应运而生，并行捕获分为并行频率捕获和并行码相位捕获。并行频率捕获是在码相位近似对齐的基础上，通过FFT运算计算出相应的多普勒频偏尖峰来实现多普勒频偏的并行捕获。并行码相位捕获则是在载波NCO近似对齐的基础上，通过FFT和IFFT运算简化载波剥离后的接收信号伪码与本地伪码之间的圆环相关运算，从而通过缩印相应的相关峰坐标值实现伪码相位延迟的并行捕获。

并行频率捕获算法

并行频率捕获算法流程图

并行频率捕获算法的流程图如下所示：
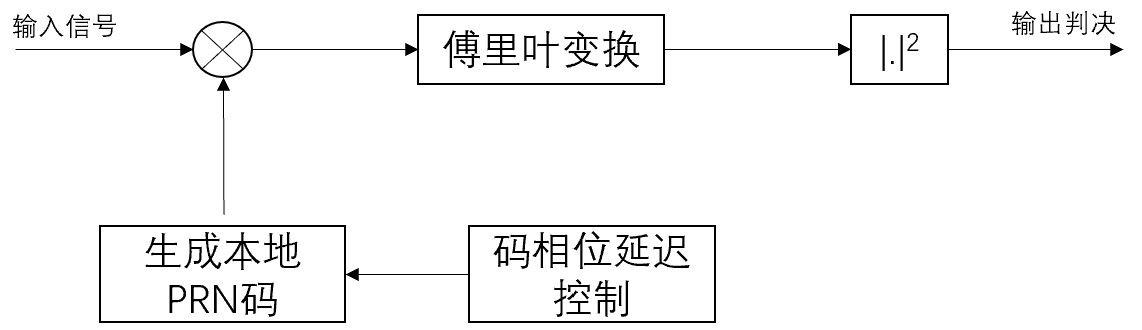
并行频率捕获

输入信号与本地产生的伪随机码相乘，并延迟本地产生的伪随机码相位为0~1023，当输入信号伪随机码与延迟特定相位的本地伪随机码对齐时，可恢复载波信号。然后对恢复的载波信号进行离散傅里叶变换或快速傅里叶变换，找出峰值，峰值所在位置对应的频率即为载波频率，减去已知的发方实际调制的载波频率即可得信号在传播途中所造成的多普勒频偏。

需要注意注意的是并行频率捕获算法的精度即为信号进行离散傅里叶变换的频率分辨率Δf=fsN\Delta f=\frac{f_s}{N}，因此要想提高并行频率捕获算法的捕获精度，要么在采样率不变的情况下延长采样时间，要么在采样时间不变的情况下增大采样率，或者一边增大采样率一边延长采样时间。

并行频率捕获算法仿真

仿真时设置接收信号的多普勒频偏为6kHz，并且扩频伪码延迟了666个码片，本地已知两颗卫星所采用的C/A码，其中一个与接收信号的伪码一致模拟并行频率捕获成功捕获的场景，另一个本地伪码则用来模拟捕获失败的场景。

具体的仿真结果如下所示：

捕获成功

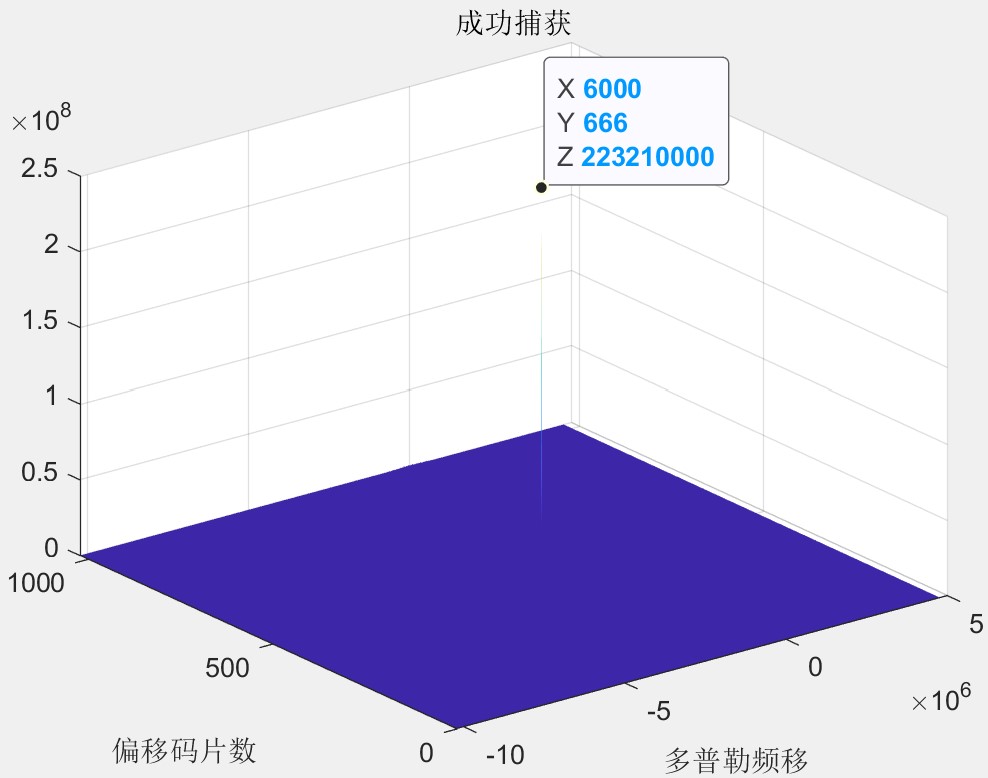
由图可得，捕获成功时会出现一个尖锐的捕获峰，从而获得接收信号的伪码延迟与多普勒频偏的估计值，仿真结果符合实验预期。

捕获失败

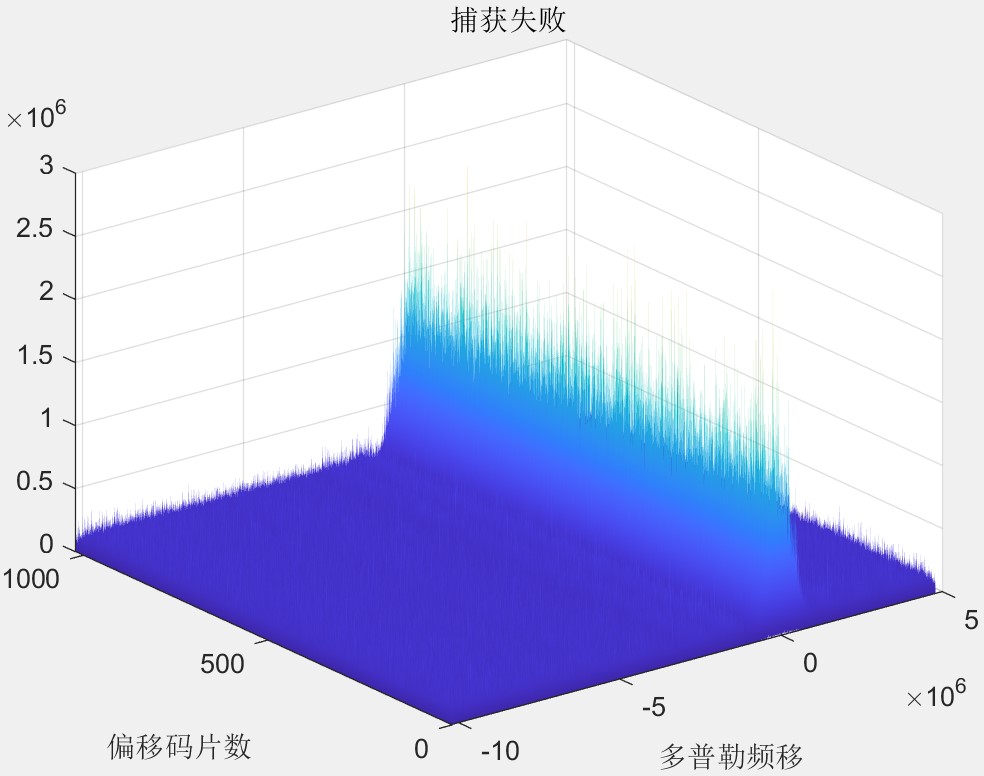
捕获失败时则不会出现明显的捕获峰，无法获得接收信号的伪码延迟与多普勒频偏的估计值。

具体的matlab仿真代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
clc;clear;close all;
f_clk=1.023e6;    %寄存器时钟脉冲频率即码片速率
fs=30e6;    %系统仿真采样率设定
t=0:(1/fs):((1e-3)-1/fs);    %系统仿真时间设定(1ms)
f_i=f_clk*10;    %输入的数字中频频率
fd_i=6e3;    %多普勒频偏
code_phase_move=666;    %伪码相位延迟
code_phase_step=0:1:1022;    %伪码相位搜索步长
tags = [[2 6];[3 7];[4 8];[5 9];[1 9];[2 6];[1 8];[2 9];[3 10];[2 3];...
    [3 4];[5 6];[6 7];[7 8];[8 9];[9 10];[1 4];[2 5];[3 6];[4 7];...
    [5 8];[6 9];[1 3];[4 6];[5 7];[6 8];[7 9];[8 10];[1 6];[2 7];...
    [3 8];[4 9]];    %G2码相位选择

[wave_CA_1,code_CA_1]=CAcode_generation(tags(6,:),f_clk,[t(1),t(end)],fs);    %本地伪码1
[wave_CA_2,code_CA_2]=CAcode_generation(tags(12,:),f_clk,[t(1),t(end)],fs);    %本地伪码2
wave_carrier_transmit=cos(2*pi*(f_i+fd_i)*t);
wave_transmit=circshift(wave_CA_1,round(-(1+(code_phase_move/f_clk-t(1))*fs))).*wave_carrier_transmit+randn(1,length(t));    %捕获电路输入信号
capture_result_1=zeros(length(code_phase_step),length(wave_transmit)/2);
capture_result_2=zeros(length(code_phase_step),length(wave_transmit)/2);

for i1=1:length(code_phase_step)
    wave_CA_phase_1=circshift(wave_CA_1,round(-(1+(code_phase_step(i1)/f_clk-t(1))*fs)));
    wave_CA_phase_2=circshift(wave_CA_2,round(-(1+(code_phase_step(i1)/f_clk-t(1))*fs)));
    signal_1=wave_transmit.*wave_CA_phase_1;
    signal_2=wave_transmit.*wave_CA_phase_2;
    fft_signal_1=abs(fft(signal_1)).^2;
    fft_signal_2=abs(fft(signal_2)).^2;
    capture_result_1(i1,:)=fft_signal_1(1:length(wave_transmit)/2);
    capture_result_2(i1,:)=fft_signal_2(1:length(wave_transmit)/2);
end

x_f=(0:(length(wave_transmit)-1))*fs/length(wave_transmit)-f_i;
x_f=x_f(1:length(wave_transmit)/2);
[FD,PHASE_code]=meshgrid(x_f,code_phase_step);
figure;
surf(FD,PHASE_code,capture_result_1);shading interp;
xlabel("多普勒频移");
ylabel("偏移码片数");
title("成功捕获");
figure;
surf(FD,PHASE_code,capture_result_2);shading interp;
xlabel("多普勒频移");
ylabel("偏移码片数");
title("捕获失败");

function [wave,code]=CAcode_generation(phase_tag,F_CLK,T,FS)
%参数说明：
%输入：phase_tag(G2码相位选择参数)，F_CLK(码片速率设置)，
% T(系统仿真时间设定T(1)为仿真时间零点，T(2)为仿真时间终点)，FS为系统采样频率)
% 实际输出的伪码波形对应的时间横坐标为：t=[T(1):(1/fs):(T(2)-1/fs)];
%输出：wave(伪码时域波形)，code(伪码二进制序列)
    reg_G1=-ones(1,10);    %-1代表1，1代表0
    reg_G2=-ones(1,10);    
    index_code=0;
    t_chip=1/F_CLK;
    wave=zeros(1,(T(2)+1/FS)*FS);
    code=zeros(1,(T(2)+1/FS)*F_CLK);
    for i0=1:(T(2)+1/FS)*FS
        if ((T(1)+(i0-1)/FS)>=T(1)+index_code*t_chip)
            sum_G1=reg_G1(3)*reg_G1(10);
            reg_G1(2:10)=reg_G1(1:9);
            reg_G1(1)=sum_G1;
            sum_G2=reg_G2(2)*reg_G2(3)*reg_G2(6)*reg_G2(8)*reg_G2(9)*reg_G2(10);
            reg_G2(2:10)=reg_G2(1:9);
            reg_G2(1)=sum_G2;
            index_code=index_code+1;
            code(index_code)=reg_G1(10)*reg_G2(phase_tag(1))*reg_G2(phase_tag(2));
        end
        wave(i0)=code(index_code);
    end
%     wave=-wave;
%     code=-code;
end